Вступающие в химическую реакцию вещества и ее продукты обладают разным запасом энергии. Это приводит к тому, что в ходе реакции должна выделяться теплота, если суммарная энергия продуктов меньше чем у реагентов, и, напротив, требуется дополнительная энергия из окружающей среды на образование продуктов, которые должны обладать более высоким запасом энергии по сравнению с исходными. Эти тепловые характеристики связаны с прочностью (энергией) химических связей
Таким образом, любая химическая реакция будет обладать тепловым эффектом:
Тепловой эффект — энергия (теплота), которая выделяется или поглощается в ходе протекания химической реакции. Она измеряется в килоджоулях (кДж)
Расчеты с участием теплового эффекта находят свое применение в самых различных областях химии. К примеру, они позволяют анализировать поведение веществ в разнообразных реакциях, сравнивая их энергетические параметры, а также подбирать оптимальные условия для протекания химических процессов, что имеет важное значение для достижения максимальной эффективности на промышленных установках.
Данные о теплотах реакций имеют большое значение при изучении химической кинетики, т.к. тепловые характеристики веществ сильно влияют на скорость и направление химических реакций.
Также тепловые эффекты могут использоваться в аналитической химии для качественного и количественного анализа
Классификация реакций по тепловому эффекту
Если в ходе реакции теплота выделяется (знак теплового эффекта «+»), то такая реакция является экзотермической:
2NO + O2 → 2NO2 + 114 кДж.
При окислении двух молей NO по этой реакции выделяется 114 кДж. Это связано с образованием оксида NO2 с более прочными химическими связями — их формирование энергетически выгодно, поэтому излишняя энергия выделяется в окружающую среду в виде теплоты
Если в ходе реакции теплота поглощается (знак теплового эффекта «-»), то такая реакция является эндотермической:
N2 + O2 → 2NO – 180,8 кДж
При окислении одного моля N2 поглощается 180.8 кДж. Молекула азота является крайне стабильной. Валентные связи в ней крайне прочные и для их разрыва требуются большие затраты энергии из внешней среды. Именно поэтому азот, составляющий 78% земной атмосферы, не вступает самопроизвольно во многие потенциальные химические реакции, оставаясь достаточно инертным веществом
Такие уравнения реакций, для которых указано количество выделяющейся или поглощаемой в ее ходе теплоты, называются термохимическими уравнениями
С термохимическими уравнениями можно работать как с математическими выражениями, т.е. их можно складывать, вычитать или же умножать на какое-то число. Т.к. часто тепловой эффект реакции рассматривается только для одного моля вещества, то стехиометрические коэффициенты, стоящие при других участниках реакции, могут оказываться дробными величинами. Записывать термохимические уравнения с дробными коэффициентами возможно, т.к.тепловой эффект указывается в расчете на моль вещества, т.е. эти уравнения оперируют количеством вещества, а не молекулами
СН4 +3/2О2 = СО + 2Н2О(Г) + 519,33 кДж
Правило для задач:
Как видно из этих уравнений тепловой эффект всегда пропорционален количеству одного из веществ (любого), участвующего в химической реакции. Это правило используется в расчетных задачах
Влияние изменения температуры на смещение химического равновесия
В соответствие с принципом Ле Шателье можно сказать, что:
При повышении температуры химическое равновесие системы смещается в сторону эндотермической реакции, а при понижении температуры – в сторону экзотермического процесса
H2 (г) + Cl2 (г) ⇄ 2HCl (г) + Q
Реакция является экзотермической, т.е. идёт с выделением теплоты, поэтому при нагревании ее равновесие сместится влево, в сторону исходных веществ, а при уменьшении температуры — наоборот, вправо, в сторону образования продуктов.
C4H10 (г) ⇄ C4H8 (г) +H2 (г) — Q
Реакция является эндотермической — она идет с поглощением теплоты извне, поэтому при нагревании ее равновесие сместится в сторону образования продуктов, а при уменьшении температуры — в сторону исходных веществ.
Какие выводы можно сделать из ТХУ?
- является ли реакция эндотермической или экзотермической
- позволяет проанализировать устойчивость соединений и прочность образующихся связей
- позволяет подобрать более оптимальные условия для протекания реакции
- рассчитать, какое количество вещества вступило в реакцию и какое количество продукта образовалось, если известен тепловой эффект реакции и наоборот
Существуют некоторые закономерности, которые помогают в некоторых случаях предсказать знак теплового эффекта.
Например, реакции, которые протекают самопроизвольно при нормальных условиях, чаще всего являются экзотермическими. В качестве примера можно привести горение угля. Эта реакция протекает самопроизвольно и необратимо с выделением большого количества тепла, т.е. реакция является экзотермической
Типичными экзотермическими реакциями являются:
- реакции горения
- реакции активных металлов и их оксидов с водой или с кислотами
- реакции нейтрализации между щелочами и сильными кислотами
- большинство легко протекающих реакций соединения (исключения: взаимодействие азота с кислородом и некоторые другие реакции)
Типичными эндотермическими реакциями являются:
- реакции разложения
- фотосинтез
Дополнительные термины
Отдельно выделяют теплоту образования и сгорания вещества, которые используют при описании химического соединения:
Теплота образования вещества – количество теплоты, выделяющееся при образовании 1 моль данного вещества из простых веществ.
Например, при сгорании алюминия:
2Аl + 3/2О2 → Аl2О3 + 1675 кДж
теплота образования оксида алюминия равна 1675 кДж/моль.
Если мы запишем термохимическое уравнение без дробных коэффициентов:
4Аl + 3О2 → 2Аl2О3 + 3350 кДж
теплота образования Al2O3 все равно будет равна 1675 кДж/моль, т.к. в термохимическом уравнении приведен тепловой эффект образования 2 моль оксида алюминия.
Теплота сгорания вещества – количество теплоты, выделяющееся при горении 1 моль данного вещества.
Например, при горении метана:
СН4 + 2О2 → СО2 + 2Н2О + 802 кДж
теплота сгорания метана равна 802 кДж/моль.
Иногда в некоторых физико-химических задачах требуется вычислить теплоту, которую нужно затратить на нагревание веществ до определенной температуры или для осуществления фазового перехода (например, когда меняется агрегатное состояние воды: лед-жидкость-пар). В этом случае пользуются новыми термодинамическими величинами
Удельная теплоемкость вещества — это физическая величина, которая показывает, какое количество теплоты в Дж необходимо передать веществу массой 1 кг для его нагрева на 1°C
Значения удельной теплоемкости различных веществ приводятся в справочниках. Так для воды (ж.) удельная теплоемкость равна 4200 Дж/кг*1°C
Задачи на тепловой эффект
Пример 1 задачи на расчеты с тепловым эффектом
Дано термохимическое уравнение для реакции сгорания водорода:
2H2(г) + O2(г) = 2H2O(г) + 484 кДж
Необходимо найти массу образовавшейся воды в граммах, если известно, что в ходе реакции выделилось 1479 кДж теплоты
Решение:
Из термохимического уравнения видно, что при образовании двух моль воды выделяется (т.к. реакция экзотермическая) 484 кДж теплоты. Вычислить массу, выделившейся в ходе реакции воды можно, составив простую пропорцию:
2 моль H2O — 484 кДж
x моль H2O — 1479 кДж

m(H2O) = n(H2O)*M(H2O) = 6.1 моль*18 г/моль = 110 г
Пример 2 задачи на расчеты с тепловым эффектом
В ходе реакции сгорания 8.96 л этана при нормальных условиях выделилось 588 кДж теплоты. Определите теплоту сгорания этана в этих условиях.
Теплота сгорания — это количество теплоты, которые выделится при сгорании одного моль вещества. В соответствии с этим определением запишем уравнение реакции для одного моль этана C2H6. Мы воспользуемся дробными коэффициентами:
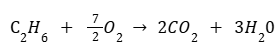
Рассчитаем количество этана в молях:
n(C2H6)=8.96/22.4 = 0.4 моль
Тогда для решения задачи достаточно составить простую пропорцию:
0.4 моль C6H6 — 588 кДж
1 моль C6H6 — x кДж
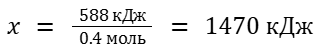
Пример 3 задачи на расчеты с тепловым эффектом
Дано термохимическое уравнение сгорания метана
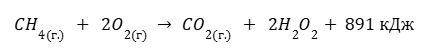
Рассчитайте количество литров (н.у) метана, которое понадобится для того, чтобы вскипятить 2л воды, которая изначально имеет температуру 20°C. Удельная теплоемкость воды равна 4200 Дж/кг*°C
Для начала найдем количество теплоты, которое нужно затратить для того, чтобы довести воду до точки кипения
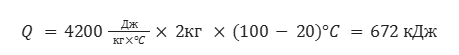
Теперь составим пропорцию
1 моль CH4 — 891 кДж
x моль CH4 — 672 кДж
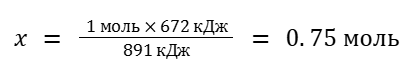
В этом случае понадобится 0.75*22.4 = 16.8 л CH4
Проверить свои знания по теме «Термохимия» можно в этом тестировании:












Новости
22.11.2024
22.11.2024
24.10.2024
14.10.2024
09.10.2024
01.10.2024